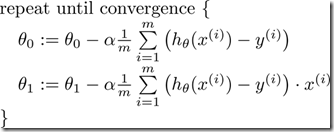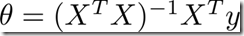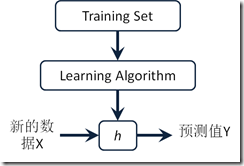
模型表示：

给定一个测试数据集，X以及X对应的标签集合Y，X为mn的矩阵，其中m代表测试集的个数，n代表测试集合的维度；Y为m1的向量，数据记录x(i, 1:n)对应y(i)，那么假设X与Y之间有关系：

Y=Xtheta+theta0，其中theta为n1的向量，theta0为余项。线性回顾的目的是要计算出一个theta与theta0用以预测以后数据的y值。在这样的theta与theta0之下，我们得到X与Y的关系函数为y=h(x)，h代表hypothesis。

为了衡量h的效果，预测误差为theta*x+theta0-y，使用J(theta,theta0)=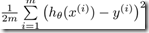 ，则我们的目的是找到这样的theta与theta0，使得J的值最小。

梯度算法

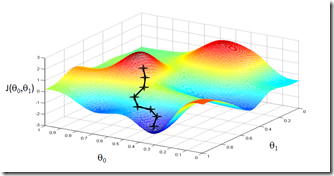
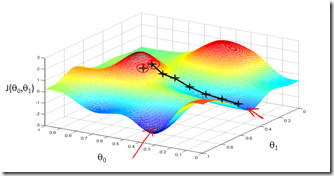
梯度算法的含义大略可以用如下图演示：（取自coursera的ppt）

梯度算法的迭代方式如下：

由于公式比较难输入，就这么讲究吧^ – ^

公式中的α决定了迭代的速度，当α比较大是，theta的收敛速度比较快，但有可能直接跳过的局部的最小值，甚至有可能荡出去而不再回来；如果α的值比较小，迭代的每一步步幅都会很小，达到极点的时间则会变长。课程上给出了一种选择恰当α的方法，通过画J-迭代次数 的图来选择，α的刻度则可以从0.00001~100之间按照数量级来更换，找到最合适的α（使得J能够收敛，并且收敛速度比较快），然后代入迭代方程中求解。

Feature Scaling

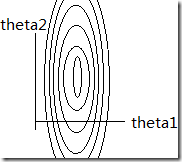
当X的维度大约2时，如果x(: , 1)与x(: , 2)之间的量纲差别过大，那么上面的两个彩图则会呈现十分扁的椭圆形，我们回归到J函数上。假设x1的尺度远大于x2的尺度，那么在J函数中其主导作用的应该是x1的值，其等高线图应该如下：

x1的坡度比较大，那么当限定了α之后，theta1的值很容易就超了，所以必须使α的值比较小，但是当α的值比较小的时候，theta2的逼近速度会非常慢。所以需要Feature Scaling技术。

常用的Feature scaling方法有如下几种：xi’ = (xi - a) / b；其中a可以为特征xi的均值，b则可以为xi的最大值、（最大值 - 最小值）、 标准差等，coursera课件上使用的是标准差。

延伸：牛顿迭代法

梯度(Gradient descent)算法是数值估计的一种，一般用于求最值，求零点，最值与零点本质上是一样的。还有一种方法叫牛顿迭代法，在高中课本（大学课本？）上曾有提过。其原理图如下：

在接近零点的时候，如果是凸性方向没有变的话（如上图），则不可能跳过零点；只用凸性方向改变的情况下才有可能跨过零点。牛顿法与梯度算法实质上的不同在于，牛顿法中（隐藏的）的α是变化的，随着切线的零点变化。

标准方程

梯度算法用于迭代估算，也可以用标准方程直接解出theta值来。方程为：

当然这里的矩阵X和theta与前文中的不太一样，X增加了一列常值1，theta增加了一个元素theta0，只是为了计算方便与样式美观。推导过程略过，在PPT的末尾讲了在何种情况下有唯一解，m>n，即元组个数比属性个数多。

然后呢

就可以用解出来的theta值进行估计了。

当然线性回归也可以解决多元多次函数，比如我们的h方程是：y=theta0+theta1x+theta2x^2+theta3*x^3，只需要在数据与处理的时候将令x1=x , x2=x^2 , x3=x^3即可。估算的时候同理，不过由于参数的次数无法在估计中完成。